プログラミング実習I : アフィン変換の補足資料
目次
1. ベクトルおよび行列
1.1. ベクトル
- ベクトルは,次式の右辺のように,いくつかの数値を縦に並べたものとして書かれる
- \(v(i)\) : ベクトル \(\vbf{v}\) の \(i\) 成分 (※ \(i\) は 1 から始まる)
- ベクトル \(\vbf{v}\) の上から \(i\) 番目の数値のこと
- 式 \eqref{eq:v} においては \(v(1) = 1\) となる
- プログラムでベクトルを扱うためには
- ベクトルの各成分を一次元配列(要素数 = ベクトルの成分数)に格納
- 例えば,以下のように,式 \eqref{eq:v} の \(\vbf{v}\) の各成分を 上から 順番に配列 v に格納していく
- つまり,\(v(i)\) を v[i-1] に代入していく
- 例えば,以下のように,式 \eqref{eq:v} の \(\vbf{v}\) の各成分を 上から 順番に配列 v に格納していく
- ベクトルの各成分を一次元配列(要素数 = ベクトルの成分数)に格納
// ベクトル v の成分を格納 double[] v = new double[3]; v[0] = 0; v[1] = 1; v[2] = 2;
1.2. 行列
- 行列は,次式の右辺のように,いくつかの数値を縦と横に並べたものとして書かれる
- 縦と横に 3 つずつ数値を並べた行列のことを 3x3 の行列と呼ぶ
- \(A(i, j)\) : \(\vbf{A}\) の \((i, j)\) 成分 (※ \(i\) および \(j\) は 1 から始まる)
- 行列 \(\vbf{A}\) の上から \(i\) 番目および左から \(j\) 番目の数値のこと
- R9 で作成する Matrix3 クラスを用いて 3x3 の行列を扱うためには
- Matrix3 クラスのオブジェクトを作成し,作成したオブジェクトのフィールド a (二次元配列) に行列の各成分を格納
- 例えば,以下のように,Matrix3 クラスのオブジェクト A を作成し,式 \eqref{eq:A} の 3x3 の行列 \(\vbf{A}\) の各成分を 左上から 順番に 二次元配列 A.a に格納していく
- つまり,\(A(i, j)\) を A.a[i-1][j-1] に代入していく
// 行列 A の成分を格納 Matrix3 A = new Matrix3(); A.a[0][0] = 0; A.a[0][1] = 1; A.a[0][2] = 2; A.a[1][0] = 3; A.a[1][1] = 4; A.a[1][2] = 5; A.a[2][0] = 6; A.a[2][1] = 7; A.a[2][2] = 8;
1.3. 行列とベクトルの積
- 行列とベクトルの積はベクトルとなる
- そのため,上記の行列 \(\vbf{A}\) とベクトル \(\vbf{v}\) の積を,あるベクトル \(u\) に等しいと書くことができる
- 3x3行列とベクトルの積の計算式 (Matrix クラス作成の TODO その 1)
式 \eqref{eq:u} で与えられるベクトル \(\vbf{u}\) の \(i\) 成分 \(u(i)\) は次式で計算できる
\begin{align} u(i) = \sum_{k = 1}^3 A(i, k)\,v(k) \label{eq:multi_v} \end{align}- \(A(i, k)\) : 行列 \(\vbf{A}\) の \((i, k)\) 成分
- \(v(k)\) : ベクトル \(\vbf{v}\) の \(k\) 成分
- 計算例
- 式 \eqref{eq:multi_v} を用いると,ベクトル \(\vbf{u}\) の計算結果は次のようになる
- R9 で作成する Matrix3 クラスを用いて,行列とベクトルの積を行うためには
- Matrix3 クラスの times メソッド(※ 引数が一次元配列のもの) を呼び出す
- 以下の例では,行列 \(\vbf{A}\) とベクトル \(\vbf{v}\) の積を計算し,その結果を一次元配列 u に格納している
- A : 行列 \(\vbf{A}\) の各成分が格納された Matrix3 クラスのオブジェクト
- v : ベクトル \(\vbf{v}\) の各成分が格納された一次元配列
// 行列 A とベクトル v の積 double[] u = A.times(v);
1.4. 行列の積
- 行列と行列の積は,行列となる
- そのため,式 \eqref{eq:A} の行列 \(\vbf{A}\) と以下の行列 \(\vbf{B}\) の積を,ある行列 \(\vbf{C}\) に等しいと書くことができる
- 3x3 行列と 3x3 行列の積の計算式(Matrix クラス作成の TODO その 2)
式 \eqref{eq:C} で与えられる行列 \(\vbf{C}\) の \((i, j)\) 成分 \(C(i, j)\) は次式で計算できる
\begin{align} C(i, j) = \sum_{k = 1}^3 A(i, k)\,B(k, j) \label{eq:multi_AB} \end{align}- \(A(i, k)\) : 行列 \(\vbf{A}\) の \((i, k)\) 成分
- \(B(k, j)\) : 行列 \(\vbf{B}\) の \((k, j)\) 成分
- 計算例
- 式 \eqref{eq:multi_v} を用いると \(C(1, 2)\) は次のようになる
- 全ての成分の計算は省略するが,行列 \(C\) の計算結果は次のようになる
- R9 で作成する Matrix3 クラスを用いて,行列と行列の積を行うためには
- Matrix3 クラスの times メソッド(※ 引数が Marix3 クラスのオブジェクトのもの) を呼び出す
- 以下の例では,行列 \(\vbf{A}\) と行列 \(\vbf{B}\) の積を計算し,その結果を Matrix3 クラスのオブジェクト C に格納している
- A : 行列 \(\vbf{A}\) の各成分が格納された Matrix3 クラスのオブジェクト
- B : 行列 \(\vbf{B}\) の各成分が格納された Matrix3 クラスのオブジェクト
- 注意事項
- 一般的に,行列積 \(\vbf{A}\,\vbf{B}\) と行列積 \(\vbf{B}\,\vbf{A}\) は等しくない
- そのため,B.times(A) と A.times(B) の結果は一般的に異なる(間違えないように!)
- 一般的に,行列積 \(\vbf{A}\,\vbf{B}\) と行列積 \(\vbf{B}\,\vbf{A}\) は等しくない
// 行列 A と行列 B の積を計算 Matrix3 C = A.times(B);
1.5. 複数の行列とベクトルの積
以下のような,2 つの行列とベクトルの積を考える
\begin{align} \vbf{u} = \vbf{A}\,\vbf{B}\,\vbf{v} \end{align}- 2 つの積への分解を繰り返すことで計算できる
- 2 つの積への分解には,以下の 2 つのパターンがある(どちらで計算しても計算結果は同じ)
- 方法 1 : \(\vbf{u} = \vbf{A} \left(\vbf{B}\,\vbf{v}\right)\) に分解して計算する方法
まず,以下の行列とベクトルの積を計算する
\begin{align} \vbf{w} = \vbf{B}\,\vbf{v} \end{align}次に,以下を計算する
\begin{align} \vbf{u} = \vbf{A}\,\vbf{w} \end{align}- R9 で作成する Matrix3 クラスを用いて,方法 1 に基づく計算を行うためには
- Matrix3 クラスの times メソッド(※ 引数が一次元配列のもの)を 以下のように 2 回呼び出す
- 以下の例では,積 \(\vbf{A}(\vbf{B}\,\vbf{v})\) を計算し,その結果を一次元配列 u に格納している
- A : 行列 \(\vbf{A}\) の各成分が格納された Matrix3 クラスのオブジェクト
- B : 行列 \(\vbf{B}\) の各成分が格納された Matrix3 クラスのオブジェクト
w : 積 \(\vbf{B}\,\vbf{v}\) の結果が格納された一次元配列
// 分解の方法 1 による 2 つの行列とベクトルの積の計算 double[] w = B.times(v); // w <- Bv double[] u = A.times(w); // u <- Aw
- 方法 2 : \(\vbf{u} = \left(\vbf{A} \vbf{B}\right) \vbf{v}\) に分解して計算する方法
まず,以下の行列積を計算する
\begin{align} \vbf{C} = \vbf{A}\,\vbf{B} \end{align}次に,以下を計算する
\begin{align} \vbf{u} = \vbf{C}\,\vbf{v} \end{align}- R9 で作成する Matrix3 クラスを用いて,方法 2 に基づく計算を行うためには
- Matrix3 クラスの times メソッド(※ 引数が Matrix3 クラスと一次元配列のもの)を以下のように 1 回ずつ呼び出す
- 以下の例では,積 \((\vbf{A}\,\vbf{B})\vbf{v}\) を計算し,その結果を一次元配列 u に格納している
- A : 行列 \(\vbf{A}\) の各成分が格納された Matrix3 クラスのオブジェクト
- B : 行列 \(\vbf{B}\) の各成分が格納された Matrix3 クラスのオブジェクト
C : 積 \(\vbf{A}\,\vbf{B}\) の結果が格納された Matrix3 クラスのオブジェクト
// 分解の方法 2 による 2 つの行列とベクトルの積の計算 Matrix3 C = A.times(B); // C <- AB double[] u = C.times(v); // u <- Cv
- 方法 1 : \(\vbf{u} = \vbf{A} \left(\vbf{B}\,\vbf{v}\right)\) に分解して計算する方法
- 行列の数が 3 つ以上ある場合も,同様に 2 つの積への分解を繰り返すことで計算できる
例えば,以下の 3 つの行列 \(\vbf{A}_i\) が存在する場合
\begin{align} \vbf{u} = \vbf{A}_2\,\vbf{A}_1\,\vbf{A}_0\,\vbf{v} \end{align}- 上の方法 1 のように分解して計算する場合
- → \(\vbf{u} = \vbf{A}_2 ( \vbf{A}_1 (\vbf{A}_0 \vbf{v}))\) として計算する
- ※ 行列とベクトルの積を 3 回行うことになる
- → \(\vbf{u} = \vbf{A}_2 ( \vbf{A}_1 (\vbf{A}_0 \vbf{v}))\) として計算する
- 上の方法 2 のように分解して計算する場合
- → \(\vbf{u} = (\vbf{A}_2 ( \vbf{A}_1 \vbf{A}_0))\, \vbf{v}\) とする
- ※ 行列と行列の積を 2 回行った後に,行列とベクトルの積を行うことになる
- → \(\vbf{u} = (\vbf{A}_2 ( \vbf{A}_1 \vbf{A}_0))\, \vbf{v}\) とする
2. アフィン変換
2.1. 概要
- アフィン変換とは?
- 平面上のある座標 \((x_0, y_0)\) を別の座標 \((x_1, y_1)\) に移す際に用いられる変換
- 参考: URL
- アフィン変換の例
- 平行移動
- 座標 \((x_0, y_0)\) を \((x_0 - 50, y_0 - 100)\) に移す
- 平行移動
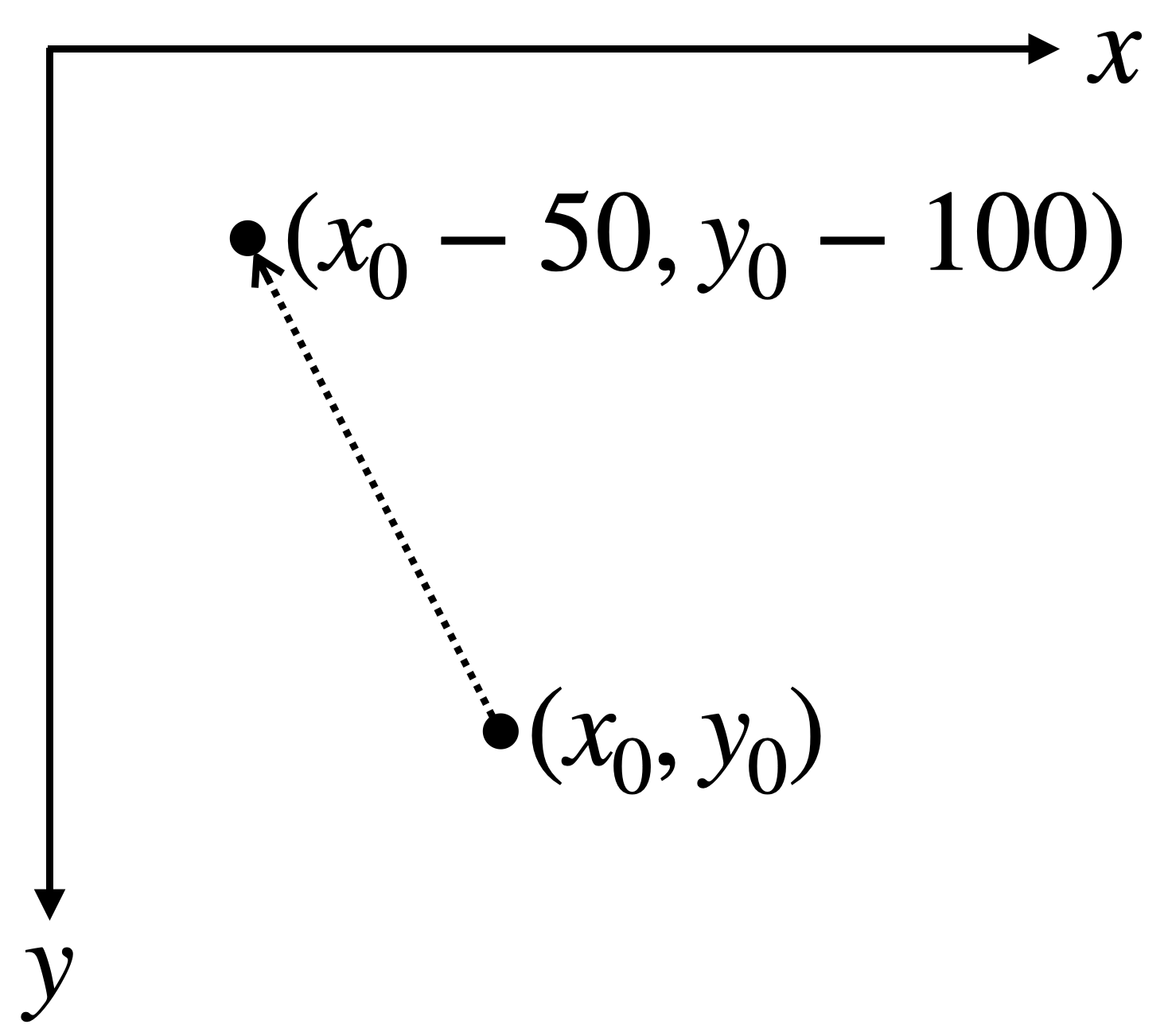
図1: 平行移動の例 (\(tx = -50\) および \(ty = -100\) の場合)
- 拡大縮小
- 座標 \((x_0, y_0)\) を \((2x_0, 3y_0)\) に移す
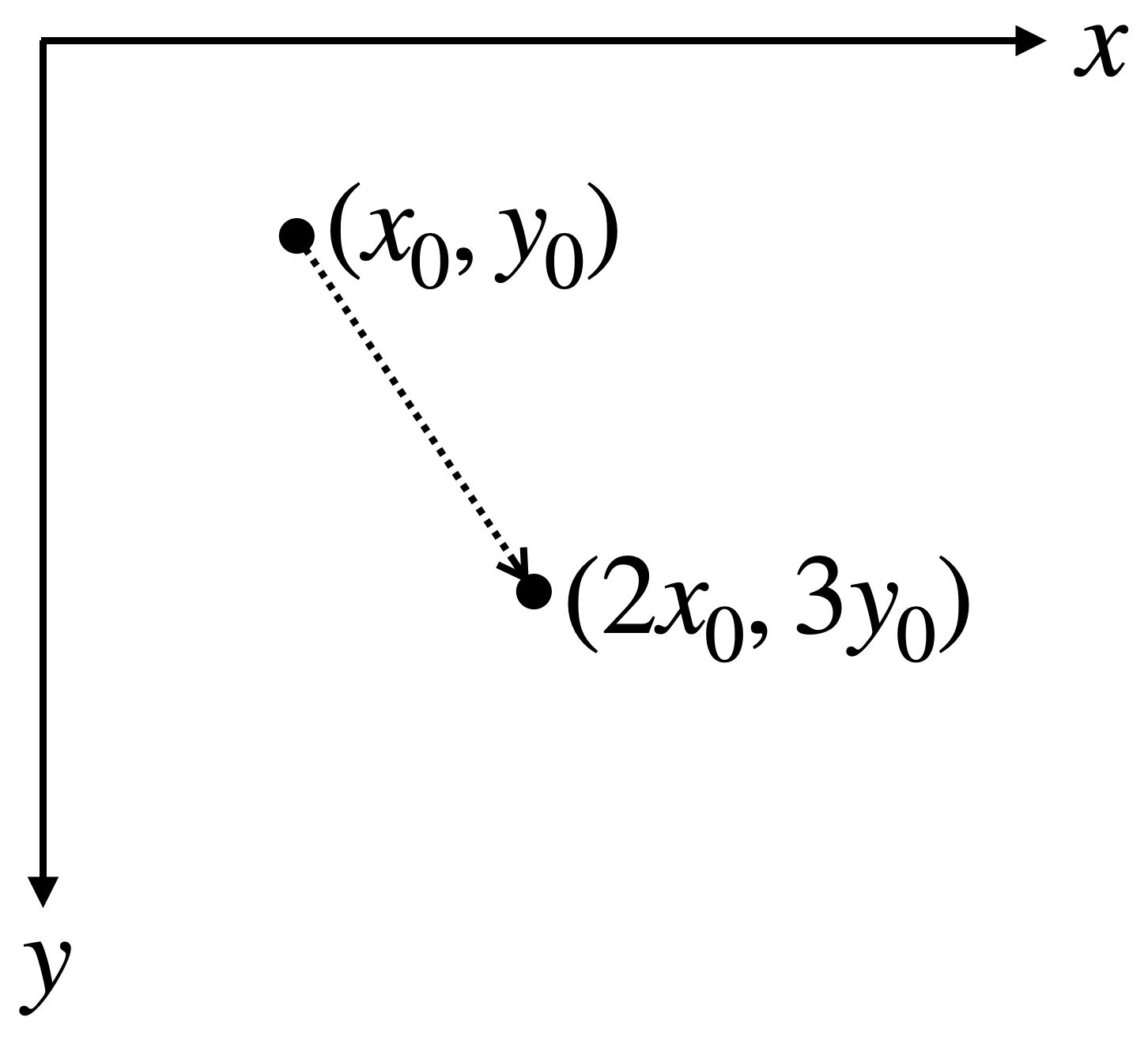
図2: 拡大縮小の例 (\(sx = 2\) および \(sy = 3\) の場合)
- 回転
- 座標 \((x_0, y_0)\) を,原点を基点として 45 度回転させた座標に移す
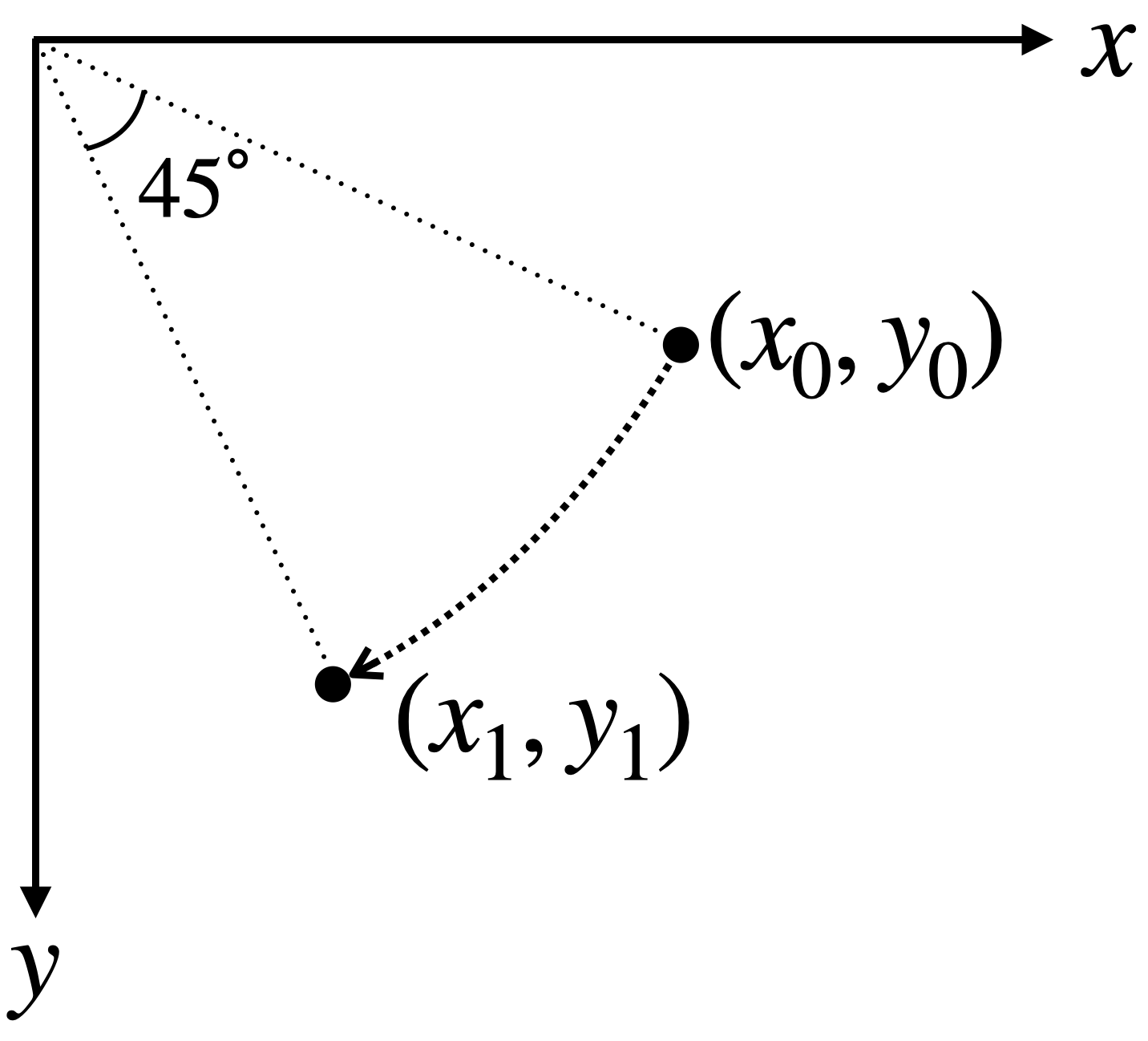
図3: 回転の例 (\(\theta = \pi/4\) (= 45°) の場合)
- 行列積とアフィン変換の関係
座標 \((x_0, y_0)\) を成分に持つ以下のベクトル \(\vbf{v}\) を考える
\begin{align} \vbf{v} &= \begin{pmatrix} x_0 \\ y_0 \\ 1 \\ \end{pmatrix} \end{align}- ※ 一番下になぜ 1 を入れるのか?の理由を知りたい人は,参考サイト を参照すること
アフィン変換で移した座標 \((x_1, y_1)\) は,ある 3x3 の行列 \(\vbf{M}\) を用いて次式で計算される
\begin{align} \begin{pmatrix} x_1 \\ y_1 \\ 1 \\ \end{pmatrix} = \vbf{M}\,\vbf{v} \end{align}- 上式のような行列 \(\vbf{M}\) のことを, 変換行列 と呼ぶことにする
- 変換行列 \(\vbf{M}\) の例として,以降の項で説明する行列 \(\vbf{T}\) や \(\vbf{S}\) ,\(\vbf{R}\) が挙げられる
- R9 で作成する Matrix3 クラスを用いてアフィン変換を行うためには
- 以下の例のように記述すればよい
- v : 座標 (x0, y0) を格納した一次元配列
- M : アフィン変換の変換行列の各成分が格納された Matrix3 クラスのオブジェクト
- 以下の例のように記述すればよい
// 座標 (x0, y0) に対してアフィン変換を行う例 double[] v = {x0, y0, 1}; double[] u = M.times(v); // u <- Mv double x1 = u[0]; double y1 = u[1];
2.2. 平行移動の変換行列
- \(x\) 軸方向および \(y\) 軸方向に \((tx, ty)\) だけ平行移動させる変換行列 \(\vbf{T}\) は次式で与えられる
2.3. 拡大縮小の変換行列
- \(x\) 軸方向に \(sx\) 倍,\(y\) 軸方向に \(sy\) 倍させる拡大縮小に対する変換行列 \(\vbf{S}\) は次式で与えられる (Matrix クラス作成の TODO その 3)
2.4. 回転の変換行列
- 原点を基点として,\(\theta\) 回転させる変換行列 \(\vbf{R}\) は次式で与えられる (Matrix クラス作成の TODO その 4)
- ※ ただし,\(\theta\) の単位はラジアン
- プログラムで行列 \(\vbf{R}\) を記述するためのポイント
- deg [°] から theta [ラジアン] に単位を変換するためには,以下を行う
double theta = Math.toRadians(deg);
- 三角関数 cos(theta) および sin(theta) を計算するには,以下のメソッドをそれぞれ用いる
- ただし theta の単位はラジアン
double x = Math.cos(theta); double y = Math.sin(theta);
2.5. 複数の変換を一度に行う合成変換
- 複数のアフィン変換を一度に行うことを 合成変換 と呼ぶ
- 合成変換に対応する変換行列は,それぞれのアフィン変換に対応する変換行列の積で与えられる
- 例えば,平行移動(tx=50, ty=50) → 拡大縮小(sx=2, sy=3) → 平行移動(tx=-30, 50) に対する合成変換を考える
- それぞれのアフィン変換に対応する変換行列を以下とする
- \(\vbf{T}_0\) : 平行移動(tx=50, ty=50) の変換行列
- \(\vbf{S}\) : 拡大縮小(sx=2, sy=3) の変換行列
- \(\vbf{T}_1\) : 平行移動(tx=-50, ty=50) の変換行列
- この例での合成変換に対応する変換行列 \(\vbf{M}\) は以下で与えられる
- アフィン変換を行う順序とは逆に,左から順番に変換行列を並べていくことに注意
- それぞれのアフィン変換に対応する変換行列を以下とする
- 例えば,平行移動(tx=50, ty=50) → 拡大縮小(sx=2, sy=3) → 平行移動(tx=-30, 50) に対する合成変換を考える
- 合成変換によって,座標 \((x_0, y_0)\) を座標 \((x_1, y_1)\) に移すためには以下を行えばよい
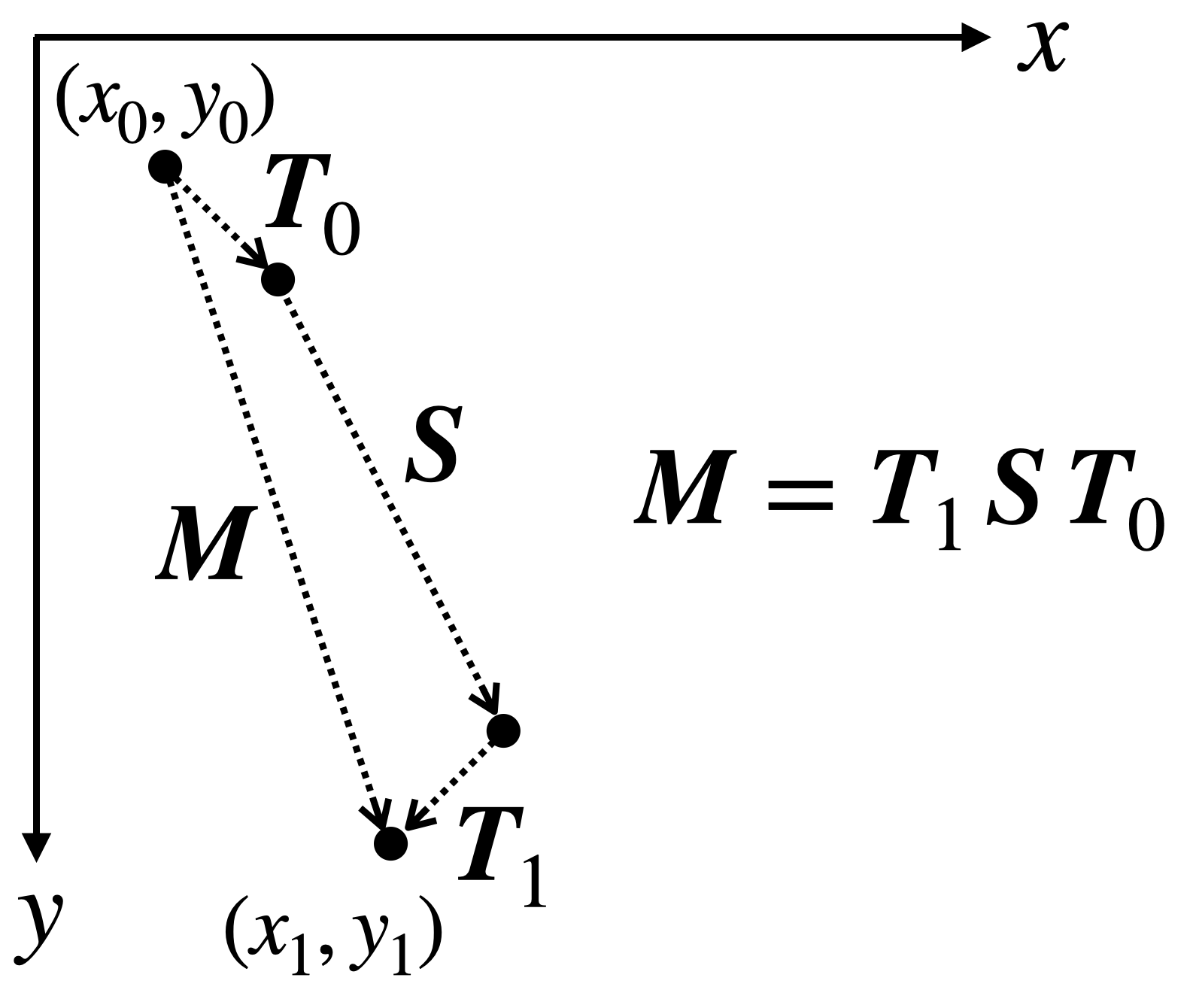
図4: 合成変換の例 (平行移動(tx=50, ty=50) → 拡大縮小(sx=2, sy=3) → 平行移動(tx=-50, 50) の場合)
- R9 で作成する Matrix3 クラスを用いて複数のアフィン変換を一度に行うためには
- 以下のように記述すればよい
- v : 座標 (x0, y0) を格納した一次元配列
- T0 : 平行移動(tx=50, ty=50) の変換行列の各成分が格納された Matrix3 クラスのオブジェクト
- S : 拡大縮小(sx=2, sy=3) の変換行列の各成分が格納された Matrix3 クラスのオブジェクト
- T1 : 平行移動(tx=-50, ty=50) の変換行列の各成分が格納された Matrix3 クラスのオブジェクト
- (x1, y1) : 変換後の座標
- 以下のように記述すればよい
// 複数のアフィン変換を一度に行う例 double[] v = {x0, y0, 1}; Matrix3 T0 = Matrix3.getT(50, 50); // 平行移動(tx = 50, ty = 50) の変換行列を作成 Matrix3 S = Matrix3.getS(2, 3); // 拡大縮小(sx = 2, sy = 3) の変換行列を作成 Matrix3 T1 = Matrix3.getT(-50, 50); // 平行移動(tx = -50, ty = 50) の変換行列を作成 // 合成変換に対応する変換行列 M を作成 Matrix3 A = S.times(T0); // A <- S T0 Matrix3 M = T1.times(A); // M <- T1 A // 合成変換(平行移動→拡大縮小→平行移動 を一度に行う) double[] u = M.times(v); double x1 = u[0]; // 変換後の x 座標を取り出す double y1 = u[1]; // 変換後の y 座標を取り出す
- 合成変換に対応する変換行列 M を作成するメリット
- 同じ変換を何度も行う場合,作成した変換行列 M を再利用することで計算時間を削減できる
- 参考: 複数のアフィン変換を一度に行わない場合
- 以下のようになる
// 複数のアフィン変換を一度に行わない例(1つずつアフィン変換を行う例) double[] v = {x0, y0, 1}; Matrix3 T0 = Matrix3.getT(50, 50); // 平行移動(tx = 50, ty = 50) の変換行列を作成 Matrix3 S = Matrix3.getS(2, 3); // 拡大縮小(sx = 2, sy = 3) の変換行列を作成 Matrix3 T1 = Matrix3.getT(-50, 50); // 平行移動(tx = -50, ty = 50) の変換行列を作成 // 1つずつアフィン変換をしていく double[] w = T0.times(v); // w <- T0 v ※ 平行移動(tx = 50, ty = 50) double[] z = S.times(u); // z <- S w ※ 拡大縮小(sx = 2, sy = 3) double[] u = T1.times(z); // u <- T1 z ※ 平行移動(tx = -50, ty = 50) double x1 = u[0]; // 変換後の x 座標を取り出す double y1 = u[1]; // 変換後の y 座標を取り出す
2.6. 多角形に対する変換
- \(n\) 個の頂点を持つ多角形に対してアフィン変換を行うことを考える
- 座標 \((x_i, y_i)\) : 多角形を構成する頂点 i の座標 (\(i = 0, .., n-1\))
- 多角形を平行移動させる例
- 以下の図のように,平行移動に対応する変換行列 \(\vbf{T}\) を用いて,すべての頂点 \(i\) の座標 \((x_i, y_i)\) を移せばよい
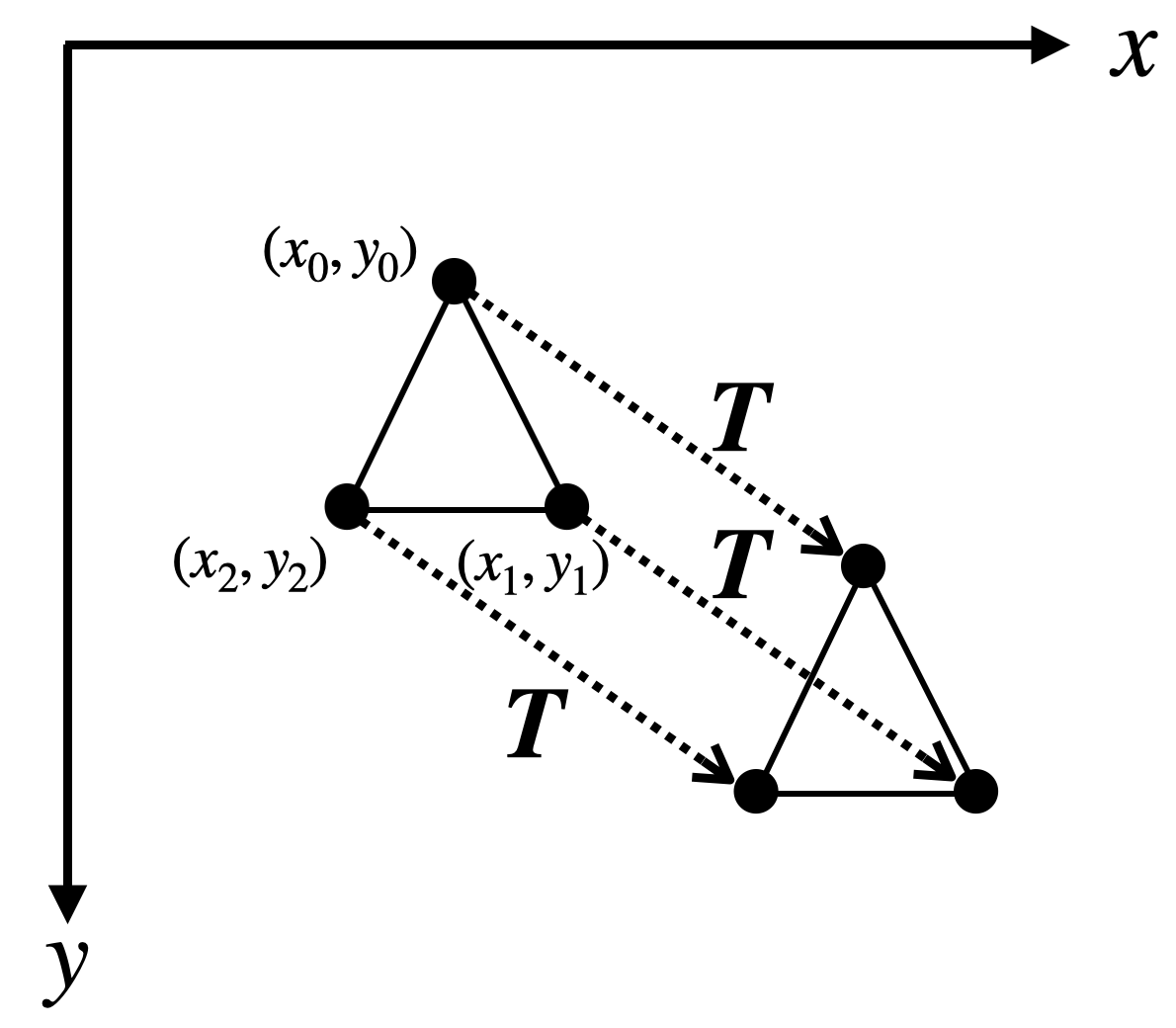
図5: 多角形の平行移動の例
- R9 で作成する Matrix3 クラスを用いて多角形に対するアフィン変換を行うためには
- 以下のように記述すれば,多角形に対するアフィン変換が行え,変換後の各頂点の座標が xPoints および yPoints に格納される
- nPoints: 多角形の頂点数
- xPoints: 各頂点の \(x\) 座標を格納した一次元配列(変換後に上書きされる)
- yPoints: 各頂点の \(y\) 座標を格納した一次元配列(変換後に上書きされる)
- M : アフィン変換の変換行列の各成分を格納した Matrix3 クラスのオブジェクト
- 以下のように記述すれば,多角形に対するアフィン変換が行え,変換後の各頂点の座標が xPoints および yPoints に格納される
// 多角形に対するアフィン変換を行う for(int i = 0; i< nPoints; i++) { double[] v = {xPoints[i], yPoints[i], 1}; // 現在の頂点 i の座標を格納 double[] u = M.times(v); // u <- Mv (頂点 i の座標をアフィン変換) xPoints[i] = u[0]; // 変換後の頂点 i の x 座標に上書き yPoints[i] = u[1]; // 変換後の頂点 i の y 座標に上書き }
3. より詳しく内容を理解したい人のために
3.1. ヨビノリ 線形代数シリーズ
- 線形代数入門 1
- 線形代数入門 2
- 線形代数入門 3