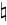DCP HOME

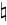Inventory Problem: L-convex minimization

We consider the initial procurement problem for a reparable inventory system [1,2]. We assume that the steady state number of items in the replenishment cycle has a Poisson distribution.

n: number of items

n =

penalty: Penalty of a backorder

penalty =

cost: Spare purchases cost of a unit of item j(j = 1, 2, ... ,n)
rate: Steady state Poisson demand rates, 0 < rate(j = 1, 2, ... ,n)

j 1 2 3
cost
rate

(Note: "Reset" button resets your inputs to default values.
An inappropriate input value will be replaced with a random number.)


We minimize the following cost function f(x): objfunc,
where x: Spare amount of item j, 0 ≤ x(j = 1, 2, ... ,n)

The first term is the backorder penalty which is computed as the cost per backorder times the steady-state expected number of maximum backorders among the items. The second term is the cost of spares purchases.

This function is L-convex [3].

This web application minimizes f(x) using ODICON with IFF by Satoru Iwata.

[1] B.L. Miller (1971): A multi-item inventory model with joint backorder criterion, Operations Research, Vol. 19, pp. 1467-1476.

[2] B.L. Miller (1971): On minimizing nonseparable functions defined on the integers with an inventory application, SIAM J. on Appl. Math., Vol. 21, pp. 166-185.

[3] S. Moriguchi and K. Murota (2005): Discrete Hessian matrix for L-convex functions, IEICE Trans. Fundamentals of Electronics, Communications and Computer Sciences, Vol. E88-A, pp. 1104-1108.

Satoko Moriguchi, Nobuyuki Tsuchimura